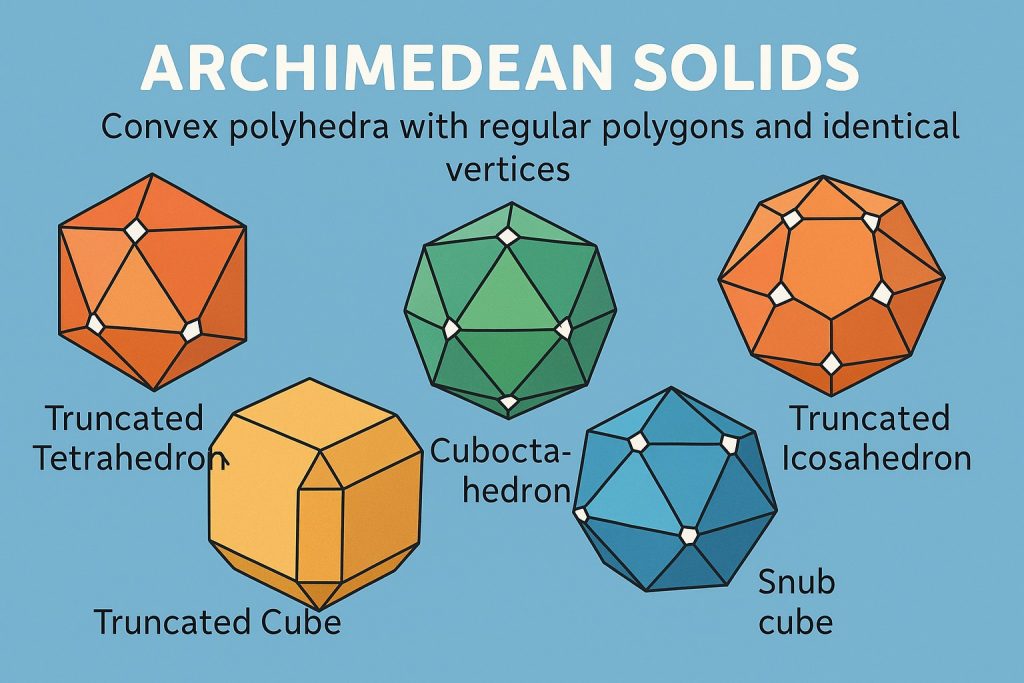
Archimedean solids are a set of 13 unique three-dimensional polyhedra named after the ancient Greek mathematician Archimedes. These shapes represent a fascinating middle ground between the perfectly regular Platonic solids and the more complex irregular polyhedra. What makes Archimedean solids special is their mathematical harmony and aesthetic beauty, which continue to captivate mathematicians, artists, and architects alike.
What Are Archimedean Solids?
An Archimedean solid is a convex polyhedron with the following properties:
- All faces are regular polygons (equilateral triangles, squares, hexagons, etc.)
- There are two or more types of regular polygons used on each solid
- All vertices (corners) are identical in arrangement—each vertex has the same combination of surrounding faces
- The shapes are highly symmetrical, but not as restricted as Platonic solids
There are exactly 13 Archimedean solids, not counting mirror images or prisms.
The 13 Archimedean Solids
Here are a few well-known examples:
| Name | Faces | Face Types |
|---|---|---|
| Truncated tetrahedron | 8 | 4 triangles, 4 hexagons |
| Cuboctahedron | 14 | 8 triangles, 6 squares |
| Truncated cube | 14 | 8 triangles, 6 octagons |
| Snub cube | 38 | 6 squares, 32 triangles |
| Truncated icosahedron | 32 | 12 pentagons, 20 hexagons (shape of a soccer ball) |
These solids can be formed by truncating (cutting off) the corners or edges of Platonic solids.
History and Discovery
- Although Archimedes first described these solids over 2,000 years ago, his original work was lost.
- The shapes were rediscovered and formalized by Johannes Kepler in the 17th century.
- Today, they are also referred to as semiregular polyhedra.
Where Are Archimedean Solids Found?
Archimedean solids appear in both natural and man-made contexts:
- Chemistry: Certain molecular and crystal structures mimic these geometries.
- Architecture and design: Used in geodesic domes, lamps, and modern structures.
- Games and sports: Dice and soccer balls are often modeled after these solids.
- Mathematical art: Celebrated in the works of M.C. Escher and modern generative artists.
Their symmetry and uniformity make them ideal for both visual appeal and structural stability.
Difference from Platonic and Catalan Solids
| Type of Solid | Faces | Vertex Uniformity | Face Uniformity |
|---|---|---|---|
| Platonic | One type | Yes | Yes |
| Archimedean | Multiple types | Yes | No |
| Catalan | One type | No | Yes |
Catalan solids are the duals of Archimedean solids—each face corresponds to a vertex of the Archimedean solid.
Glossary
- Polyhedron — A 3D solid with flat polygonal faces.
- Truncation — The process of cutting off the vertices or edges of a shape.
- Convex — A shape where all interior angles are less than 180°, and it curves outward.
- Vertex-transitive — All corners (vertices) look the same from a geometric perspective.
- Dual — A related solid where vertices and faces are swapped.